05:00
What is clustering, anyway?
EPID 684
Spatial Epidemiology
University of Michigan School of Public Health
Jon Zelner
[email protected]
epibayes.io

Agenda
What is a hotspot 🔥, anyway?.
Discussing the idea of kernel smoothing and how it relates to Tobler’s 1st Law.
Hands-on with some smoothing models.
On your own
Spend a few minutes answering these questions:
Based on the readings, how would you describe what a disease cluster is?
When might you undertake a cluster study? Is there a difference between a disease cluster and a hotspot ?
What are some challenges or pitfalls of cluster analysis?
Why might one undertake a cluster-based study?
Public Health Response.
Hypothesis testing.
Identifying key causal mechansisms.
Reasoning about clusters is tricky
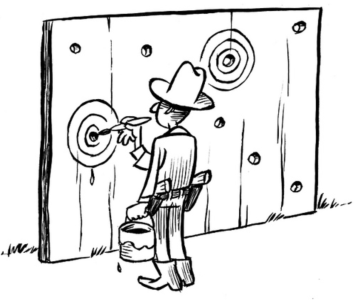
The Texas Sharpshooter 🎯 Problem is an example of a logical fallacy that can come up in the analysis of spatial clusters.
What is a hotspot?



A hotspot is often in the eye of the beholder…
More detail is necessary to make the hotspot concept useful
We recommend that the meaning of a “hotspot” be made explicit by use of an appropriate modifier such as: “burden hotspot,” to denote areas of elevated disease prevalence or incidence; “transmission” or “risk hotspot,” to denote areas of elevated transmission efficiency or a higher risk of disease acquisition; and “emergence hotspot,” to denote areas with an increased probability of disease emergence or reemergence. (Lessler et al., 2017)
A cluster can represent multiple facets 💎 of risk
Spatial aggregation of a disease outcome.
Clustering of a specific exposure risk.
Evidence of social processes that concentrate disadvantage and multiple risks.
Smoothing!
Smoothing lets us separate signal 📡 from noise 📣
Often used to describe or uncover clusters.
What are some examples of a spatial signal or information?
What are some possible sources of noise that could obscure the signal?
What are some risks associated with mistaking noise \(\to\) signal?
A guided tour of smoothing approaches
Next Time
