When working with spatial data, our analytic task often falls into either of two rough categories.
Estimating local averages of a continuous variable. This could be something like neighborhood-by-neighborhood variation in average blood pressure or the intensity of some kind of environmental risk factor such as the intensity of fine (e.g. \(PM_{2.5}\)) dust which can cause respiratory illness.
Estimating the local density of or incidence of a particular outcome. For example, if we are trying to understand spatial variation in the incidence of a particular disease, we are interested in knowing how many cases of that disease are present in a given location or are likely to be present in some nearby unobserved location.
In this tutorial, we’ll dig into the problem of spatial density estimation in one dimension along a spatial transect. The techniques discussed here form the basis of a number of approaches for cluster or hotspot analysis. For examples of smoothing local values of a continuous variable, check out this tutorial.
A motivating example
A spatial transect is an area of space along a line crossing a landscape. These are often used in ecology and forestry to assess the health of an environment, species diversity and other factors. Using a transect can help simplify the problem of spatial analysis down to one dimension rather than the usual two, while still providing a tremendous amount of useful information.
Example of an ecological transect from the US National Park Service (source)
For example, (Levy et al. 2014) were interested in characterizing the intensity of exposure to triatomine bugs and other insect vectors of the pathogen T. cruzi, which causes Chagas disease.
Triatoma (left- and right-hand panels) and T. cruzi (center) (source)
Intensity of Triatomine infestation along a 2km transect in Arequipa, Peru (Figure from Levy et al. (2014))
Imagine we are estimating the density of some unknown insect vector along a 1 kilometer transect with the goal of characterizing the risk of infection with a vector-borne illness.
Kernel density estimation in one dimension
Much like in our discussion of kernel smoothing of continuous outcomes, kernel functions play a key role in this setting as well. In this case, imagine that the locations of vectors along our transect have been sampled at random from some unknown function \(f(x)\) which takes values from 0 (the beginning of the transect) to 1000m (the end).
We can use the Kernel function \(K(d)\) to approximate the intensity of the outcome of interest at each observed case location \(x_i\). Imagine that our observed data have locations \(x_1, x_2, \ldots, x_n\) and that the distance between our point of interest, \(x_j\) and each observed point is \(d_{ij} = | x_j - x_i |\).
Finally, lets include a bandwidth parameter, \(h\), which controls the width of the window we will use for smoothing. When we put this all together, we can get an estimate of the density of our outcome of interest at location \(x_j\) as follows:
As you can see below, we can pick a range of kernel functions, but for the sake of simplicity, in this example, we will focus in on a Gaussian, or normal, kernel, which uses the probability density function of a normal distribution to weight points.
Lets start by sampling locations of observed points along a one dimensional line. To keep things interesting, we’ll use a Gaussian mixture distribution with two components:
First, lets imagine a scenario in which the risk of observing an insect vector steadily decreases as we walk along our transect. However, along the way there is a hotspot of increased risk beyond what we would expect from the smooth decline before and after that spot. For the purpose of this example, we’ll assume that risk decays exponentially with distance from the origin, but that our hotspot is centered at a point 300 meters into the transect. The code below lets us sample the locations of the points along the transect where 🐜 are observed from two distributions:
An exponential distribution representing smooth decay from the beginning to the end of the transect, and
A normal distribution representing a hotspot about 150m in width beginning 300m in
The figure below shows a histogram of locations sampled from \(f(x)\) (vertical bars) overlaid with the true value of \(f(x)\) in red:
Now, imagine we have another set of finely spaced points along the line, and for each, we want to calculate the weight for each. The function below lets us do that:
The figure below shows the true value of our density function \(f(x)\) in red, the density of points in the simulated data along the x-axis of the ‘rug plot’, and our smoothed density in black, for a bandwidth of \(h=10\):
You can adjust the range of the bandwidth here to get a better sense of the relationship between the smoothed curve (black) and true density (red). Adjust the bin width for the histogram of the underlying data to get a sense of the fit of the model to the underlying data.
viewof h = Inputs.range([1,100], {value:10,step:2,label:"Bandwidth (m)"})viewof bw = Inputs.range([5,100], {value:10,step:5,label:"Bin width (m)"})viewof kern = Inputs.select(["gaussian","uniform","tricube","triangular"], {value:"gaussian",label:"Smoothing kernel"})numbins =Math.floor(1000/bw)dtrans =transpose(hvals)Plot.plot({y: {grid:true,label:"Density"},x: {label:"Distance from transect start (m) →"},marks: [ Plot.rectY(transpose(sample),Plot.binX({y:"count"}, {x:"loc",fill:"steelblue",thresholds: numbins})), Plot.lineY(dtrans, {filter: d => (d.h== h) && (d.smoother== kern),curve:"linear",x:"x",y: d => d.y* bw}), Plot.lineY(transpose(dens), {x:"x",y: d => d.y* bw,curve:"linear",stroke:"red"}) ]})
The figure below shows the relative amount of weight placed on different points as a function of their distance from the point of interest (0, marked by the vertical red line):
kv =transpose(kernvals).filter(d => d.h== h && d.smoother== kern)Plot.plot({y: {grid:true,label:"Relative weight of point as compared to origin"},x: {label:"Distance from point of interest (m) ↔ "},marks: [//Plot.lineY(kv, {filter: d => (d.smoother == kern), x:"x", y: d => d.y*1000}),Plot.lineY(kv, Plot.normalizeY({x:"x",y:"y",basis:"extent"})),Plot.ruleX([0], {stroke:"red"})]})
Questions
Which of the bandwidth options seems to do the best job in capturing the value of \(f(x)\)? Why?
How does the choice of kernel impact the smoothing?
How do the different kernel functions encode different assumptions about distance decay?
What is the relationship between the histogram of the data and the smoother? What do you see as you change the histogram bin width relative to the smoothing bandwidth?
Levy, Michael Z., Corentin M. Barbu, Ricardo Castillo-Neyra, Victor R. Quispe-Machaca, Jenny Ancca-Juarez, Patricia Escalante-Mejia, Katty Borrini-Mayori, et al. 2014. “Urbanization, Land Tenure Security and Vector-Borne Chagas Disease.”Proceedings of the Royal Society B: Biological Sciences 281 (1789): 20141003. https://doi.org/10.1098/rspb.2014.1003.
Citation
BibTeX citation:
@online{zelner2023,
author = {Zelner, Jon},
title = {Making Sense of Spatial Density Estimation},
date = {2023-01-26},
url = {https://zelnotes.io/posts/spatial-density},
langid = {en}
}
---title: "Making sense of spatial density estimation"author: "Jon Zelner"date: "1/26/2023"categories: - code - tutorial - statistics - spatial - Rimage: kde_example.pngbibliography: refs.bibexecute: cache: true---When working with spatial data, our analytic task often falls into either of two rough categories.1. *Estimating local averages of a continuous variable.* This could be something like neighborhood-by-neighborhood variation in average blood pressure or the intensity of some kind of environmental risk factor such as the intensity of fine (e.g. $PM_{2.5}$) dust which can cause respiratory illness.2. *Estimating the local density of or incidence of a particular outcome.* For example, if we are trying to understand spatial variation in the incidence of a particular disease, we are interested in knowing how many cases of that disease are present in a given location or are likely to be present in some nearby unobserved location.In this tutorial, we'll dig into the problem of spatial density estimation in one dimension along a spatial *transect*. The techniques discussed here form the basis of a number of approaches for cluster or hotspot analysis. For examples of smoothing local values of a continuous variable, check out [this tutorial](/posts/smoothing/index.qmd).## A motivating exampleA spatial transect is an area of space along a line crossing a landscape. These are often used in ecology and forestry to assess the health of an environment, species diversity and other factors. Using a transect can help simplify the problem of spatial analysis down to one dimension rather than the usual two, while still providing a tremendous amount of useful information. )](transect.png.png){width=60%}For example, [@levy2014] were interested in characterizing the intensity of exposure to triatomine bugs and other insect vectors of the pathogen *T. cruzi*, which causes Chagas disease. )](triatomine.png.png){width=60%}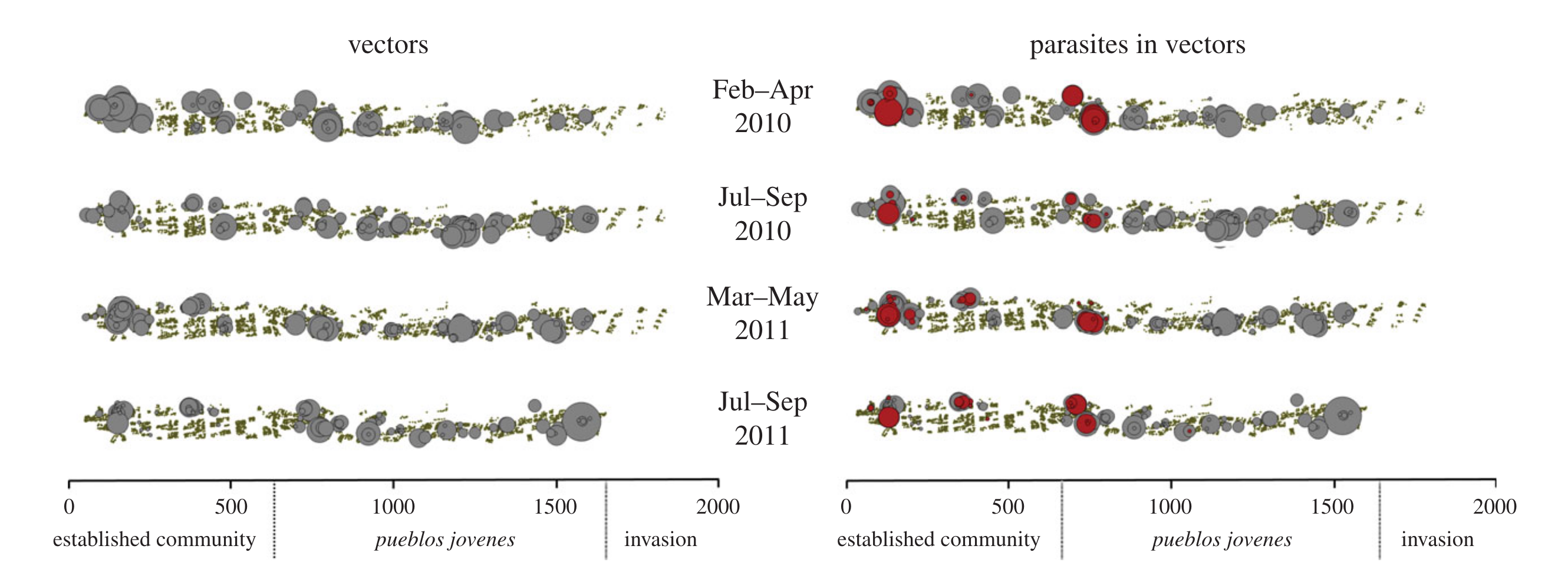Imagine we are estimating the density of some unknown insect vector along a 1 kilometer transect with the goal of characterizing the risk of infection with a vector-borne illness. ## Kernel density estimation in one dimensionMuch like in our discussion of [kernel smoothing of continuous outcomes](/posts/smoothing/index.qmd), kernel functions play a key role in this setting as well. In this case, imagine that the locations of vectors along our transect have been sampled at random from some unknown function $f(x)$ which takes values from 0 (the beginning of the transect) to 1000m (the end).We can use the Kernel function $K(d)$ to approximate the intensity of the outcome of interest at each observed case location $x_i$. Imagine that our observed data have locations $x_1, x_2, \ldots, x_n$ and that the distance between our point of interest, $x_j$ and each observed point is $d_{ij} = | x_j - x_i |$.Finally, lets include a bandwidth parameter, $h$, which controls the width of the window we will use for smoothing. When we put this all together, we can get an estimate of the density of our outcome of interest at location $x_j$ as follows:$$\hat{f_h}(x_j) = \frac{1}{n} \sum_{i=1}^{n} K(\frac{x_j - x_i}{h})$$As you can see below, we can pick a range of kernel functions, but for the sake of simplicity, in this example, we will focus in on a Gaussian, or normal, kernel, which uses the probability density function of a normal distribution to weight points. Lets start by sampling locations of observed points along a one dimensional line. To keep things interesting, we'll use a Gaussian mixture distribution with two components:)](kernel-comparison.png){width=60%} ## Worked exampleFirst, lets imagine a scenario in which the risk of observing an insect vector steadily decreases as we walk along our transect. However, along the way there is a *hotspot* of increased risk beyond what we would expect from the smooth decline before and after that spot. For the purpose of this example, we'll assume that risk decays *exponentially* with distance from the origin, but that our hotspot is centered at a point 300 meters into the transect. The code below lets us sample the *locations* of the points along the transect where 🐜 are observed from two distributions:1. An exponential distribution representing smooth decay from the beginning to the end of the transect, and2. A normal distribution representing a hotspot about 150m in width beginning 300m in```{r}#| echo: false#| warning: falserequire(dplyr)## Sample from two intensity distributionsc <-500## Number of total casesp_hot <-0.2## Proportion of cases in the hotspot c_hot <-rbinom(1, c, p_hot) ## Sample the exact number of hotspot casesc_not <- c-c_hot ## The number of non-hotspot cases.x_a <-rexp(c_not, rate =1/250) ## Sample the locations of non-hotspot casesx_b <-rnorm(c_hot, mean =300, sd =50) ## Sample the locations of hotspot casesx <-c(x_a, x_b) ## Vector of all hotspot locationssample_df <-data.frame(id =1:length(x), loc = x) %>%filter(x <=1000)cc <-nrow(sample_df)```The figure below shows a histogram of locations sampled from $f(x)$ (vertical bars) overlaid with the true value of $f(x)$ in red:```{r}#| code-fold: true#| warning: falselibrary(ggplot2)d_a <-dexp(1:1000, rate =1/250) d_b <-dnorm(1:1000, mean =300, sd =50)y <- ((1-p_hot))*d_a + (p_hot*d_b)dens_df <-data.frame(x =1:1000, y = y)xdf <-data.frame(x=x)g <-ggplot(xdf) +geom_histogram(aes(x=x, y=..density..), bins=100) +geom_line(data=dens_df, aes(x=x,y=y), colour="red") +xlim(0, 1000) +ylab("Density") +xlab("Distance from transect origin (m)")plot(g)```Now, imagine we have another set of finely spaced points along the line, and for each, we want to calculate the weight for each. The function below lets us do that:```{r}#| warning: false#| echo: false#| code-fold: falselibrary(evmix)library(purrr)normal_smoother <-function(x, h =10, delta =1, xmin =1, xmax =1000, kern = kdgaussian, kernp=kpgaussian) {## Make a vector with the input points xj <-seq(xmin, xmax, by = delta)## Make an empty vector to store the densities xdens <-map_dbl(xj, function(xj) mean(kern(xj-x, bw=h)/kernp(xj, bw=h)))## Package everything in a dataframe to return df <-data.frame(x=xj, y=xdens)return(df)}```The figure below shows the true value of our density function $f(x)$ in red, the density of points in the simulated data along the x-axis of the 'rug plot', and our smoothed density in black, for a bandwidth of $h=10$:```{r}#| code-fold: TRUElibrary(ggplot2)pred_df <-normal_smoother(x, h =10)g <-ggplot() +geom_rug(aes(x=x)) +geom_line(data = pred_df, aes(x=x, y=y)) +ylab("Density") +geom_line(data = dens_df, aes(x=x,y=y), colour="red") +xlim(0, 1000)dens_ojs <- dens_dfdens_ojs$y <- dens_ojs$y*ccplot(g)``````{r}#| echo: false#| cache: falseojs_define(dens = dens_ojs)```Now, lets see what happens if we try this for different values of $h$:```{r}#| code-fold: TRUEall_df <-data.frame()for (hv inc(5, 10, 20, 50 ,100, 250)) { pred_df <-normal_smoother(x, h = hv) pred_df$h <- hv all_df <-rbind(all_df, pred_df) } all_df$h <-as.factor(all_df$h)g <-ggplot(all_df) +geom_rug(aes(x=x)) +geom_line(data = dens_df, aes(x=x,y=y), colour="red") +geom_line(aes(x=x, y=y)) +ylab("Density") +facet_wrap(~ h) +xlim(0, 1000)plot(g)``````{r}#| code-fold: trueall_df <-data.frame()hvals <-seq(1, 100, by =2)distvals <-seq(-100, 100, by =1)all_kernvals <-data.frame()for (hv in hvals) { pred_df <-normal_smoother(x, h = hv) pred_df$h <- hv pred_df$smoother <-"gaussian" all_df <-rbind(all_df, pred_df) all_kernvals <-rbind(all_kernvals,data.frame(x=distvals, y=kdgaussian(distvals, bw = hv), smoother ="gaussian", h = hv)) pred_df <-normal_smoother(x, h = hv, kern = kduniform, kernp=kpuniform) pred_df$h <- hv pred_df$smoother <-"uniform" all_df <-rbind(all_df, pred_df) all_kernvals <-rbind(all_kernvals,data.frame(x=distvals, y=kduniform(distvals, bw = hv), smoother ="uniform", h = hv)) pred_df <-normal_smoother(x, h = hv, kern = kdtricube, kernp=kptricube) pred_df$h <- hv pred_df$smoother <-"tricube" all_df <-rbind(all_df, pred_df) all_kernvals <-rbind(all_kernvals, data.frame(x=distvals, y=kdtricube(distvals, bw = hv), smoother ="tricube", h = hv)) pred_df <-normal_smoother(x, h = hv, kern = kdtriangular, kernp=kptriangular) pred_df$h <- hv pred_df$smoother <-"triangular" all_df <-rbind(all_df, pred_df) all_kernvals <-rbind(all_kernvals, data.frame(x=distvals, y=kdtriangular(distvals, bw = hv), smoother ="triangular", h = hv))}all_df$y <- all_df$y * cc``````{r}#| echo: false#| cache: falseojs_define(sample=sample_df)ojs_define(hvals = all_df)ojs_define(kernvals = all_kernvals)```## Trying different bandwidths and kernelsYou can adjust the range of the bandwidth here to get a better sense of the relationship between the smoothed curve (black) and true density (red). Adjust the bin width for the histogram of the underlying data to get a sense of the fit of the model to the underlying data.```{ojs}// |echo: falseviewof h = Inputs.range([1, 100], {value: 10, step: 2, label: "Bandwidth (m)"})viewof bw = Inputs.range([5, 100], {value: 10, step: 5, label: "Bin width (m)"})viewof kern = Inputs.select(["gaussian", "uniform", "tricube", "triangular"], {value: "gaussian", label: "Smoothing kernel"})numbins = Math.floor(1000/bw)dtrans = transpose(hvals)Plot.plot({y: {grid: true, label: "Density"},x: {label: "Distance from transect start (m) →"}, marks: [ Plot.rectY(transpose(sample),Plot.binX({y: "count"}, {x: "loc", fill: "steelblue", thresholds: numbins})), Plot.lineY(dtrans, {filter: d => (d.h == h) && (d.smoother == kern), curve: "linear", x:"x",y: d => d.y * bw}), Plot.lineY(transpose(dens), {x:"x", y: d => d.y * bw, curve:"linear", stroke: "red"}) ]})```The figure below shows the relative amount of weight placed on different points as a function of their distance from the point of interest (0, marked by the vertical red line):```{ojs}// |echo: falsekv = transpose(kernvals).filter(d => d.h == h && d.smoother == kern)Plot.plot({y: {grid: true, label: "Relative weight of point as compared to origin"},x: {label: "Distance from point of interest (m) ↔ "},marks: [//Plot.lineY(kv, {filter: d => (d.smoother == kern), x:"x", y: d => d.y*1000}),Plot.lineY(kv, Plot.normalizeY({x:"x", y: "y", basis: "extent"})),Plot.ruleX([0], {stroke: "red"})]})```### Questions- Which of the bandwidth options seems to do the best job in capturing the value of $f(x)$? Why?- How does the choice of kernel impact the smoothing?- How do the different kernel functions encode different assumptions about *distance decay*?- What is the relationship between the histogram of the data and the smoother? What do you see as you change the histogram bin width relative to the smoothing bandwidth?## Additional ResourcesPlease see Matthew Conlen's excellent [interactive KDE tutorial](https://mathisonian.github.io/kde/)## References