Measuring spatial and contextual variation

EPID 594
Spatial Epidemiology
University of Michigan School of Public Health

Jon Zelner
[email protected]
epibayes.io

Today’s Theme

Making the most of multi-level data using hierarchical models

Agenda

  • Brief recap of the threefold path of hierarchical modeling

  • Radon ☢️ lab 🧪 !

  • Preview of next week

Let’s extend the blood pressure model from Merlo et al. to include a risk/protective factor.

  • Simulated study where we sample 1000 individuals (\(i\)) from 20 neighborhoods (\(j\)) and measure:

  • \(y_{ij}\) is continuous systolic blood pressure (SBP) for individual \(i\) in location \(j\).

  • \(x_i \in [0,1]\) is a binary exposure indicating whether the individual gets regular physical exercise.

  • \(\beta\) is an increase in \(y_i\) associated with the exposure

  • \(\alpha\) is mean SBP in the absence of exposure

How can we deal with the fact that people are clustered within locations?

You have three choices: Which 🚪 will you choose?

Door 🚪 #1: Ignore clustering and fit a normal GLM

  • Pool data across all units, i.e. ignore clustering.

  • i.e. fit model \(y_{ij} = \alpha + \beta x_i + \epsilon_i\)

  • Is this typically a good idea?

NO!

Complete pooling ignores potential sources of observed and unobserved unit-level confounding.

Full pooling of clustered data violates assumption of independent errors

A fully pooled model:

\[ y_i = \alpha + \beta x + \epsilon_i \]

Assumes \(y_i\) is a combination of systematic variation (\(\alpha + \beta x\)) and uncorrelated random noise (\(\epsilon_i\)) where:

\[ \text{i.i.d.} \epsilon \sim Normal(0, \sigma^2) \]

Your residuals should look like this

Code 
require(ggplot2)
set.seed(1299445)
df <- data.frame(x = rnorm(1000))
g <- ggplot(df, aes(x = x)) +
  geom_histogram(binwidth = 0.1, aes(y=..density..)) +
  stat_function(fun = dnorm, args = list(mean = 0, sd = 1)) +
  xlab("Distance from mean model prediction") +
  ylab("Density") + 
  theme_bw()
plot(g)

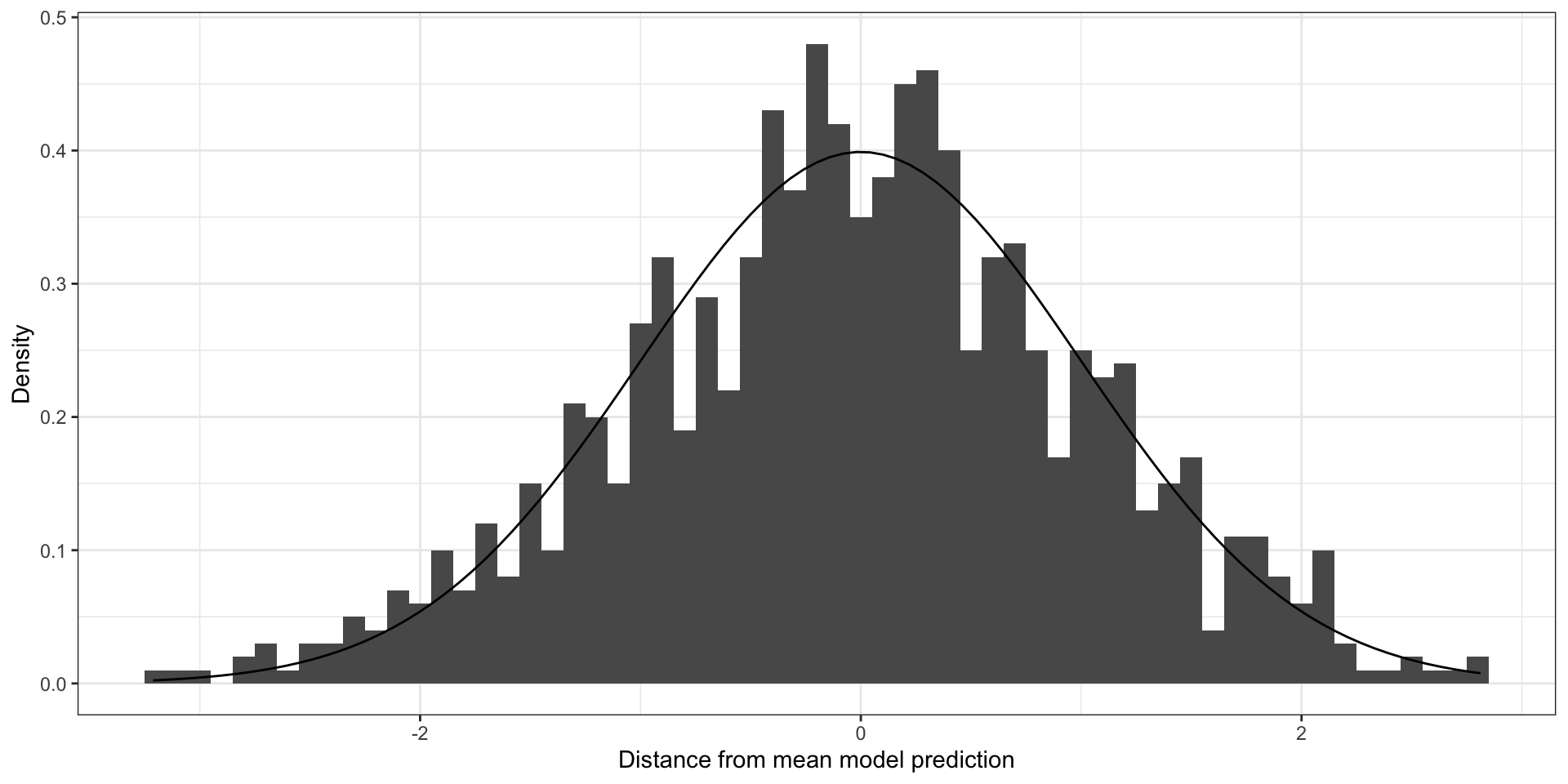
Residuals for a model with un-clustered errors

Your residuals should look like this

Code 
require(ggplot2)
g <- ggplot(df, aes(sample = x)) +
  stat_qq() +
  stat_qq_line()

plot(g)

Residuals for a model with un-clustered errors

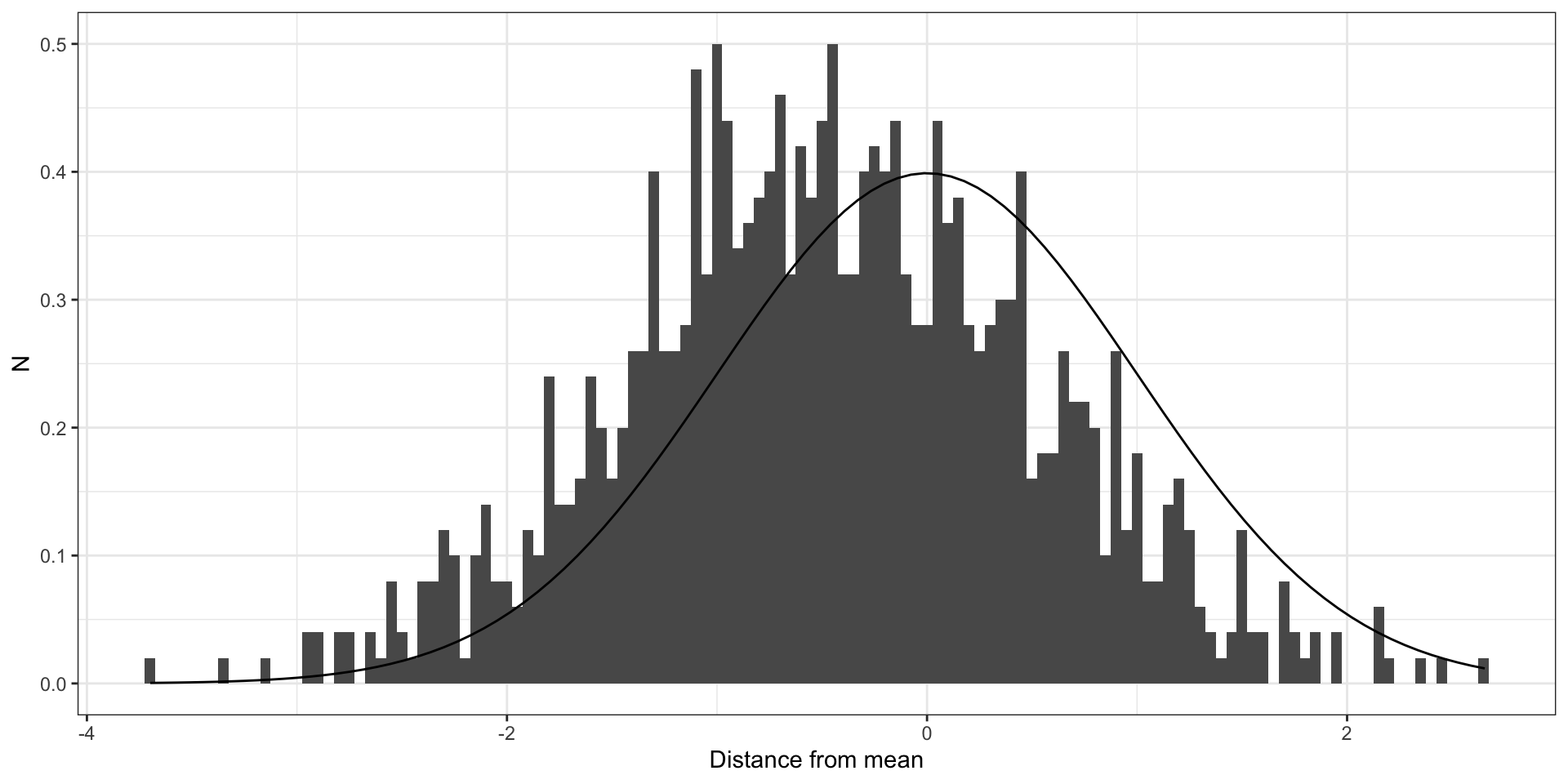
If you ignore strong 💪 clustering (ICC = 0.9)

Code 
require(ggplot2)
icc <- 0.9
total_var <- 1
cluster_sigma <- sqrt(icc * total_var)
ind_sigma <- sqrt((1 - icc) * total_var)
ind_cluster <- 100
ncluster <- 10
cluster_ids <- sort(rep(1:ncluster, ind_cluster))
cluster_means <- rnorm(ncluster, sd = cluster_sigma)
ind_vals <- rnorm(n = length(cluster_ids), mean = cluster_means[cluster_ids], sd = ind_sigma)

df <- data.frame(x = ind_vals, cluster = cluster_ids)

g <- ggplot(df, aes(x = x, cluster = cluster_ids)) +
  geom_histogram(binwidth = 0.05, aes(y=..density..)) +
  xlab("Distance from mean") +
  ylab("Density") +
  stat_function(fun = dnorm, args = list(mean = 0, sd = sqrt(total_var))) +
  theme_bw()


plot(g)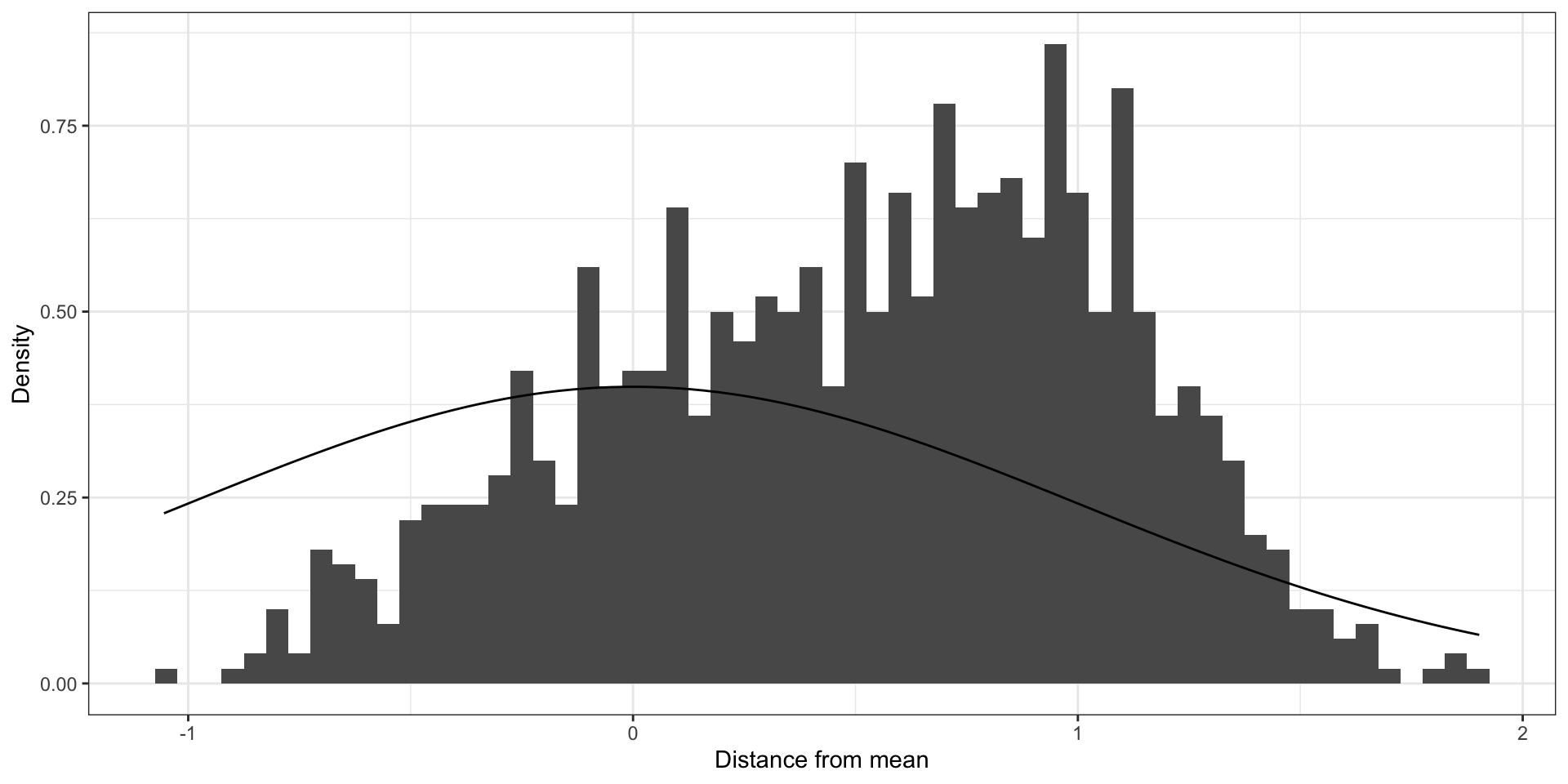

Clustered errors that are far from being normal

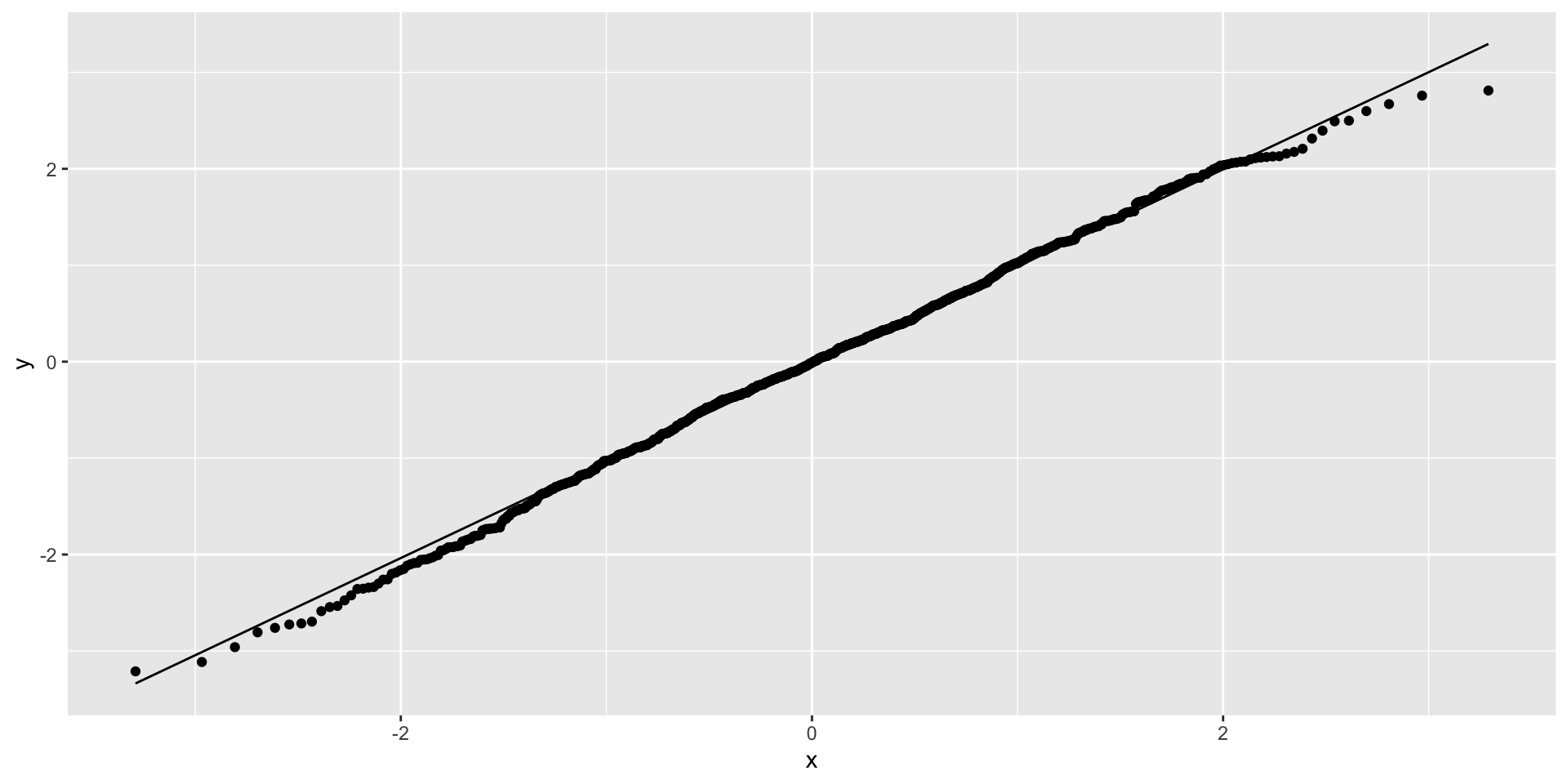
If you ignore strong 💪 clustering (ICC = 0.9)

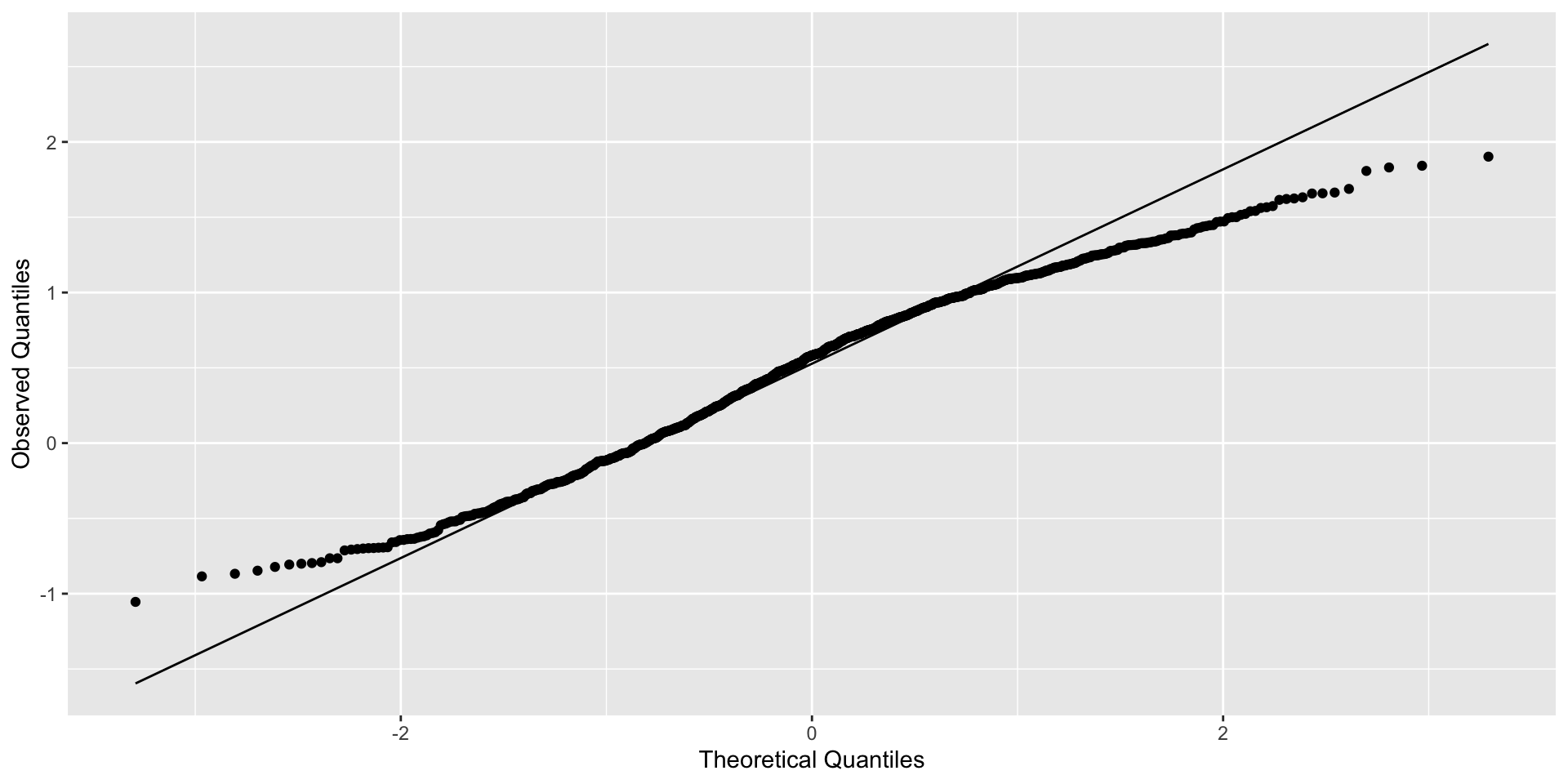
Qqplot of residuals

If you ignore moderate clustering (ICC = 0.5)

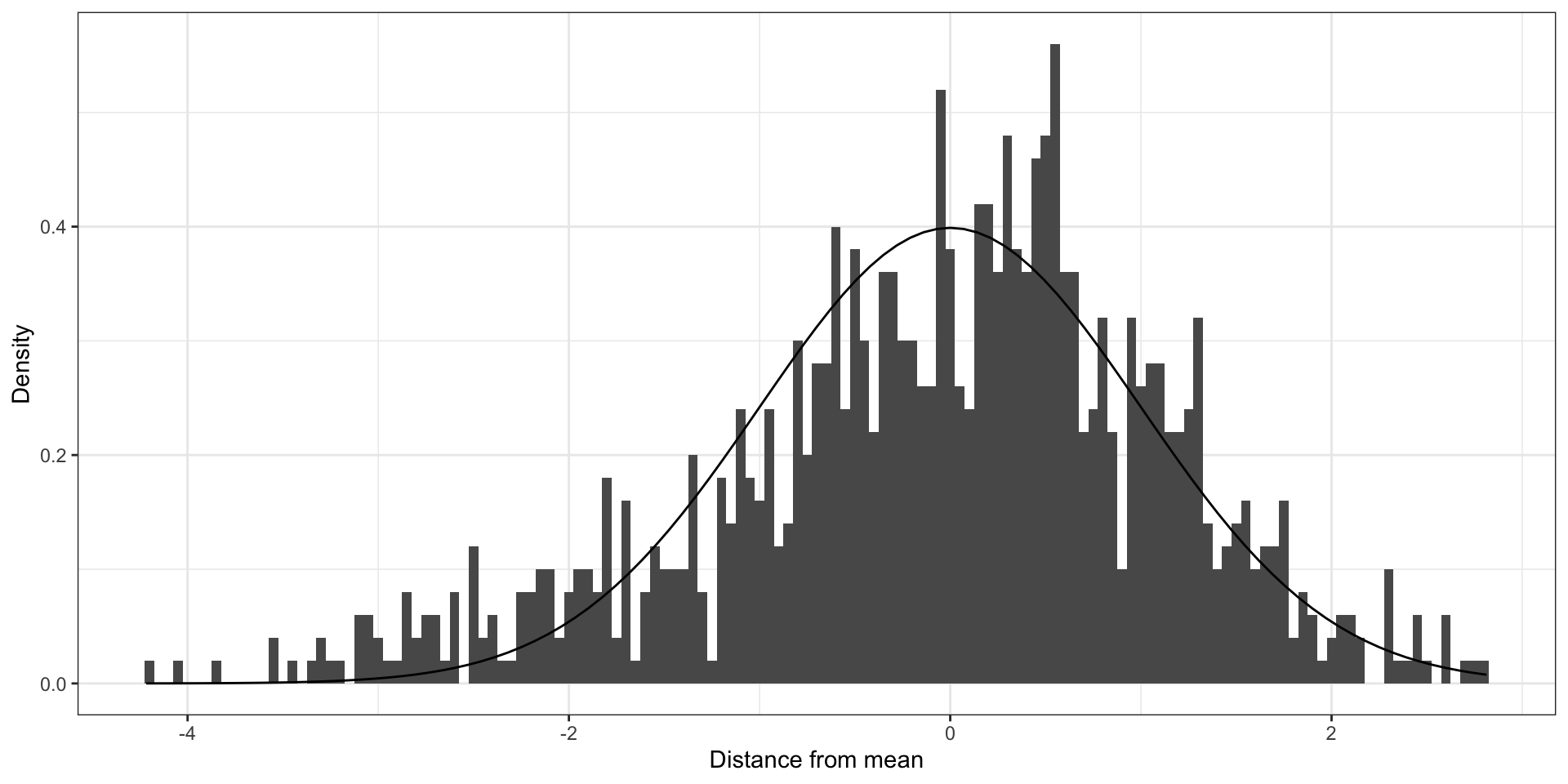
Moderately clustered errors

If you ignore moderate clustering (ICC = 0.5)

Example of residuals for model with clustered errors

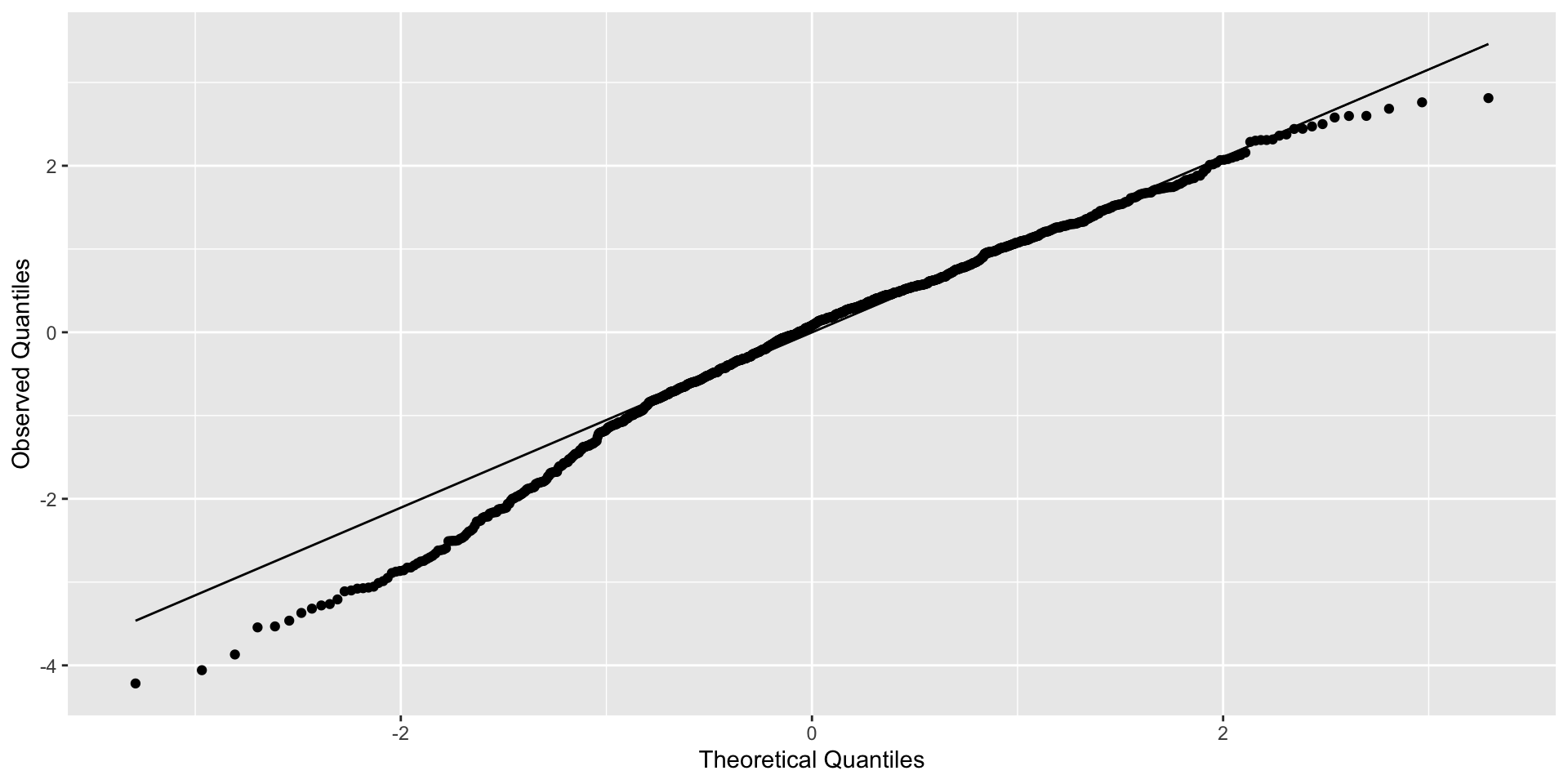
If you ignore weaker clustering (ICC = 0.25)

Clustered errors

If you ignore weaker clustering (ICC = 0.25)

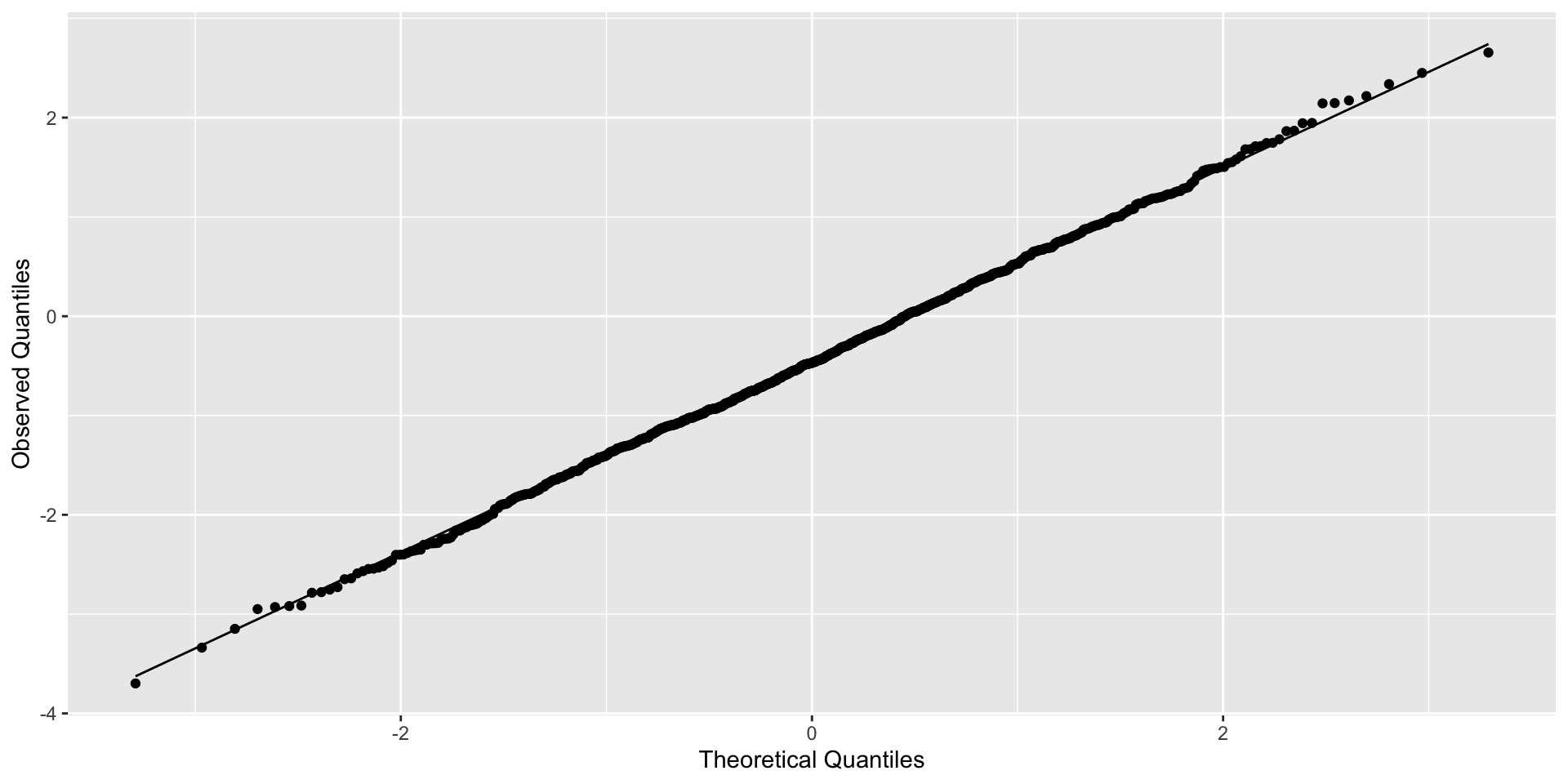
Example of residuals for model with clustered errors

Door 🚪 #2: Fit a different model to each cluster

  • Unpooled approach:Fit a separate model to each unit (\(j\)), assuming outcomes in each unit are independent:

  • Model looks like: \(y_{ij} = \alpha_j + \beta_j x_i + \epsilon_{ij}\)

  • Where: \(\epsilon_{ij} \sim N(0, \sigma_{j}^2)\)

More danger!

Totally unpooled models run the risk of overfitting the data, particularly in small samples.

Specific dangers of unpooled models

  • Some places may have few observations, making unpooled models impractical

  • We may want to allow the effect of an exposure to be consistent across location.

  • Will have nothing to say about data from a new location

How would our ideal model split the difference between fully pooled and totally unpooled?

  • Encode the assumption that places are similar unless data tell us otherwise.

  • Be flexible enough to reflect information in new data without overfitting.

  • Give answers equivalent to the fully pooled and unpooled approaches if that is what the data actually suggest.

Door 🚪 #3: Partial Pooling 🏊!

  • Allow effects to vary across clusters, but constrain them to come from the same distribution:

  • Model looks like: \(y_{ij} = \alpha + \beta x_i + \epsilon_{i} + \epsilon_{j}\)

  • Where: \(\epsilon_{i} \sim N(0, \sigma_{i}^2)\)

  • And: \(\epsilon_{j} \sim N(0, \sigma_{j}^2)\)

What does partial pooling get us?

  • This approach accommodates variation across units without assuming they have no similarity.

  • Allows us to include covariates both about individuals and their spatial context.

  • More likely to make accurate out-of-sample predictions than the fully-pooled or unpooled examples.

Radon!

Imagine you’re in the radon system business

My very own radon mitigation system!

How could you use/extend the partial pooling model from the Gelman paper to:

  1. Sell more radon systems in Minnesota?

  2. Reduce the burden of inequality in radon-associated health risks in Minnesota?

  3. Branch out into other markets, like Michigan, where we have good measurements of soil uranium but don’t have access to household-level radon measurements?

05:00

As the soil uranium ☢️ increases, so does baseline county-level radon

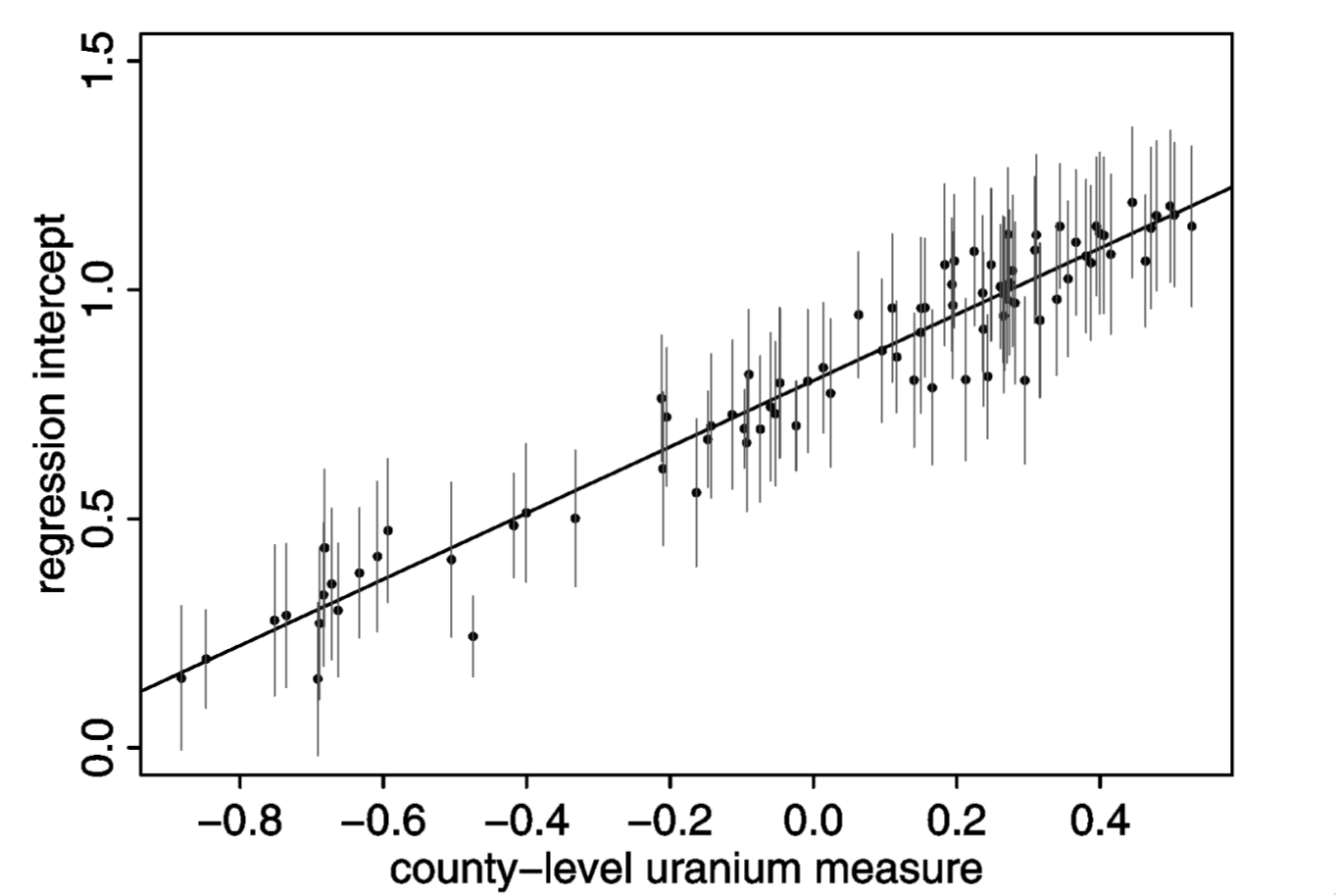
Counties with lots of soil uranium seem like a good bet for business

Partial pooling most benefits predictions for places with less data

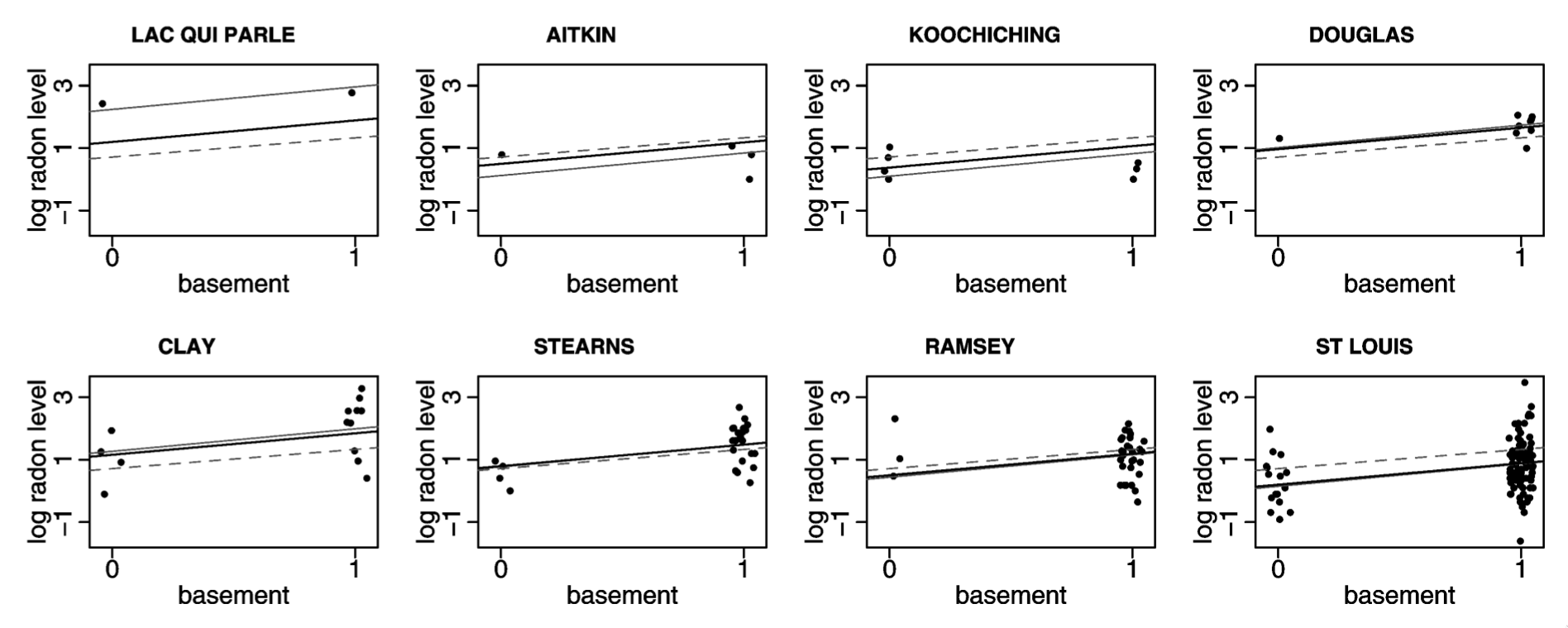
Light dotted line = full pooling; Light solid line = no pooling; Dark line = partial pooling

Time for a test-drive! 🏎️

Radon hands-on activity

Next Week

References